#suma de polinomios
Explore tagged Tumblr posts
Text
youtube
Aprenderás a sumar polinomios agrupando términos semejantes y reduciendo términos.
#suma de polinomios#polinomios#suma de polinomios algebraicos#operaciones con polinomios#reducción de términos semejantes#suma#suma y resta#suma de términos semejantes#suma y resta de polinomios#resta de términos semejantes#coeficientes#polinomios suma y resta#grado de un polinomio#grado de un monomio#terminos semejantes mismo signo#signo#signo negativo#signo positivo#cero#agrupacion de terminos#Youtube
0 notes
Text
Descomposición en fracciones parciales P/Q, Caso 1. Donde Q sólo tiene factores lineales no repetidos.
Sean las expresiones racionales: 3/ x+4 y 2/ x-3 Si en la suma de dos expresiones racionales, una expresión racional es la razón de dos polinomios, que denotaremos como P y Q, 3/ x+4 + 2/ x-3, esto se resuelve así: 3(x-3) + 2(x+4) / (x+4)(x-3) = 3x-9 + 2x+8 /x²+x-12 = 5x-1 / x²+x-12 Resultado. El procedimiento inverso, se empieza con una expresión racional 5x-1 / x²+x-12 y se descompone en…
View On WordPress
#Descomponer P/Q. Donde Q solo tiene factores lineales no repetidos. 12.5 13;14;17;18;31;32;33;43;44
0 notes
Text
¿Cómo simplificar la expresión matemática 1/x + 2?
🎰🎲✨ ¡Obtén 500 euros y 200 giros gratis para jugar juegos de casino con solo un clic! ✨🎲🎰
¿Cómo simplificar la expresión matemática 1/x + 2?
Simplificación de fracciones
La simplificación de fracciones es un concepto fundamental en matemáticas que consiste en reducir una fracción a su forma más simple. Para simplificar una fracción, se deben dividir tanto el numerador como el denominador por el máximo común divisor de ambos números.
Por ejemplo, si tenemos la fracción 8/12, podemos simplificarla dividiendo ambos números por 4, que es el máximo común divisor de 8 y 12. De esta manera, obtenemos la fracción simplificada 2/3. Esta fracción es equivalente a la fracción original 8/12, pero está expresada en su forma más simple.
Simplificar fracciones es importante porque nos permite trabajar con números más manejables y comprender mejor las relaciones entre ellos. Además, las fracciones simplificadas son más fáciles de sumar, restar, multiplicar o dividir, ya que los cálculos son más sencillos y menos propensos a errores.
Es importante recordar que no todas las fracciones se pueden simplificar. Por ejemplo, las fracciones irreducibles o fracciones en su forma más simple no pueden reducirse aún más. Es fundamental dominar el proceso de simplificación de fracciones para resolver problemas matemáticos con mayor facilidad y precisión. ¡Practica este concepto y mejora tus habilidades matemáticas!
Expresiones algebraicas
Las expresiones algebraicas son fundamentales en el estudio de las matemáticas, ya que nos permiten representar y resolver problemas de una manera más general y abstracta. Una expresión algebraica está formada por números, letras y signos matemáticos, que se combinan siguiendo ciertas reglas.
En una expresión algebraica, las letras representan números desconocidos o variables, lo que nos permite realizar operaciones matemáticas sin necesidad de conocer los valores concretos de esas variables. Por ejemplo, la expresión algebraica "3x + 7" significa que multiplicamos la variable x por 3 y luego sumamos 7 al resultado.
Las expresiones algebraicas se utilizan en una amplia variedad de contextos, desde la resolución de ecuaciones simples hasta la modelización de fenómenos complejos en física, química o economía. Al manipular expresiones algebraicas, podemos simplificar problemas, factorizar polinomios, resolver ecuaciones o despejar incógnitas en funciones matemáticas.
Es importante entender las reglas básicas de las expresiones algebraicas, como la jerarquía de operaciones, las propiedades de los números reales y las leyes de los exponentes. Con una sólida comprensión de la algebra, podemos mejorar nuestras habilidades de resolución de problemas y razonamiento matemático.
En resumen, las expresiones algebraicas son una herramienta poderosa y versátil en el mundo de las matemáticas, que nos permite abordar problemas de manera abstracta y generalizada, facilitando la resolución de una amplia gama de situaciones matemáticas y científicas.
Suma de fracciones
La suma de fracciones es una operación matemática básica que consiste en combinar dos o más fracciones para obtener un resultado único. Para poder sumar fracciones, es fundamental que tengan el mismo denominador. En caso de que las fracciones tengan denominadores diferentes, primero se deben encontrar fracciones equivalentes con el mismo denominador antes de proceder con la suma.
Para sumar fracciones con el mismo denominador, simplemente se suman los numeradores y se conserva el mismo denominador. Por ejemplo, si queremos sumar 1/4 + 1/4, el resultado sería 2/4, que simplificado sería igual a 1/2.
En el caso de sumar fracciones con distintos denominadores, primero se buscan fracciones equivalentes. Por ejemplo, si queremos sumar 1/3 + 1/6, para encontrar un denominador común multiplicamos cruzadamente los denominadores: 3 * 6 = 18. Entonces, las fracciones equivalentes serían 2/6 + 1/6 = 3/6, que simplificado sería igual a 1/2.
Es importante recordar que al sumar fracciones, el resultado final puede necesitar simplificarse para expresarlo de manera más sencilla. La suma de fracciones es una operación fundamental en las matemáticas y se aplica en diversos contextos, desde la vida cotidiana hasta la resolución de problemas más complejos en ámbitos académicos y profesionales.
Fracciones simples
Las fracciones simples son un tema fundamental en matemáticas que suele causar confusión en muchos estudiantes. Una fracción simple es aquella en la que el numerador es menor que el denominador y no se puede simplificar aún más. Por ejemplo, 1/2 es una fracción simple, ya que el numerador (1) es menor que el denominador (2) y no comparten ningún divisor común mayor que 1.
Para trabajar con fracciones simples, es importante recordar algunas reglas básicas. En primer lugar, para sumar o restar fracciones simples, es necesario que tengan el mismo denominador. Si no es así, es necesario hallar el denominador común para poder operar con ellas. Para multiplicar fracciones simples, simplemente se multiplican los numeradores entre sí y los denominadores entre sí. Para dividir fracciones, se multiplica la primera fracción por el recíproco de la segunda fracción.
Es común encontrar fracciones simples en situaciones cotidianas, como al repartir una pizza en partes iguales o al calcular porcentajes. Por lo tanto, dominar el concepto de fracciones simples es esencial para desenvolverse con soltura en diversas situaciones de la vida diaria y en estudios más avanzados de matemáticas.
En resumen, las fracciones simples son una herramienta matemática básica pero imprescindible, que nos ayuda a entender y operar con cantidades fraccionarias de manera eficiente y precisa. Dominar este concepto nos permitirá resolver problemas con mayor facilidad y precisión en diversos contextos.
Operaciones matemáticas
Las operaciones matemáticas son la base de la aritmética y juegan un papel fundamental en la resolución de problemas en la vida cotidiana, así como en campos más complejos como la física, la ingeniería y la economía. Estas operaciones incluyen la suma, la resta, la multiplicación y la división, y son fundamentales para el desarrollo de habilidades matemáticas sólidas.
La suma es una operación que consiste en combinar dos o más valores para obtener un resultado total. Por otro lado, la resta se encarga de determinar la diferencia entre dos cantidades. La multiplicación es una operación repetitiva de suma, donde una cantidad se suma varias veces, y la división es la operación inversa a la multiplicación, donde un valor se divide en partes iguales.
Es fundamental comprender la jerarquía de las operaciones matemáticas, es decir, la secuencia en la que se deben realizar las operaciones para obtener el resultado correcto. Esto se conoce como el uso de paréntesis, exponentes, multiplicación, división, suma y resta en ese orden.
Dominar estas operaciones matemáticas es esencial para resolver problemas de manera eficiente y precisa. Además, fomenta el pensamiento crítico, la lógica y la resolución de problemas, habilidades que son valiosas en todos los aspectos de la vida. Por lo tanto, es importante practicar y perfeccionar estas operaciones para fortalecer nuestra comprensión matemática y mejorar nuestro rendimiento académico y profesional.
0 notes
Text
Funciones y polinomios / 2. División entre polinomios y raíces de un polinomio
División de polinomios Las operaciones de suma, resta y multiplicación de polinomios son triviales: se llevan a cabo siguiendo las reglas algebraicas usuales. Restar los polinomios y (Sol.: ) Multiplicar los polinomios y (Sol.: La división se realiza por el método que explicamos a continuación con un Dividir el polinomio entre . Sol.: Se escriben el dividendo, , y el divisor, , como en una…

View On WordPress
0 notes
Text
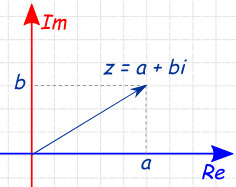
Locura Matemática Nº 1: i Es la Raíz Cuadrada de –1, Pero ¿Cuál Es la Raíz Cuadrada de i?
09 julio 2023, Chicagolandia, IL
Entonces, si recuerda el álgebra de la escuela secundaria, los números negativos no tienen raíces cuadradas que sean números reales y los números imaginarios (los números reales usados como coeficiente de la unidad imaginaria i, la raíz cuadrada de -1) se desarrollaron, en parte, para dar raíces cuadradas a estos números. (En realidad, se desarrollaron originalmente en el siglo XVI para trabajar con números imaginarios que surgirían en el camino para resolver ecuaciones cúbicas con números reales, pero poder finalmente escribir las raíces cuadradas de números reales negativos resulta ser un beneficio indirecto, pero clave.) Los números complejos son, a su vez, la suma de un número real, a, y un número imaginario, bi, y toman la forma a + bi.
Entonces, como hemos establecido, i es la raíz cuadrada de –1, pero ¿cuál es, a su vez, la raíz cuadrada de i?
En la escuela secundaria, como un adolescente, intenté responder esta pregunta, pero por alguna razón, la respuesta no me llegaba, así que inventé j como la raíz cuadrada de i. Pero entonces, ¿cuál sería la raíz cuadrada de j? Tal vez k? (Mucho más tarde, aprendí sobre los cuaterniones, números cuadridimensionales—de 4 dimensiones—de la forma a + bi + cj + dk, sin embargo, en los cuaterniones, ni j es la raíz cuadrada de i, ni k es la raíz cuadrada de j. Voy a cubrir los cuaterniones en otra publicación de este blog). De todos modos, resultó que estaba completamente en el camino equivocado.
Más tarde, mientras yo estaba en la universidad (mucho antes de descubrir los cuaterniones), resolví este problema usando el Teorema de deMoivre (la potencia de un número complejo en la forma polar, r(cos θ + i sen θ), se puede calcular por elevando r al exponente y multiplicando el mismo exponente por el ángulo: [r(cos θ + i sen θ)]ⁿ = rⁿ(cos nθ + sen nθ) ).
Sin embargo, como descubrí más tarde, encontrar la solución es incluso más fácil que eso. Todo lo que se necesita hacer es establecer el cuadrado de un número complejo genérico, z, en i, calcular el cuadrado de su forma estándar, a + bi, establecer la parte real de este cuadrado en 0 y la parte imaginaria en 1 y luego resuelve las dos ecuaciones resultantes.
(rzcuda(n) = la raíz cuadrada de n)
z² = i -> (a + bi)² = i -> a² + 2abi + b²i² = i -> a² – b² + 2abi = i (i = 0 + 1i) -> (1) a² – b² = 0, (2) 2abi = i -> 2ab = 1
(1) a² – b² = 0 -> (a + b)(a – b) = 0 -> (1A) a + b = 0 -> a = –b, (1B) a – b = 0 -> a = b:: (1) a = ±b
(2) 2ab = 1 -> ab = 1/2 -> aplicando (1B) -> b² = 1/2 -> (2A) b = ±1/rzcuda(2) -> aplicando (1B) al revés: b = a -> (2B) a = ±1/rzcuda(2), aplicando (1A) a (2) -> –bb = 1/2 -> –b² = 1/2 -> (2C) bi = ±1 /rzcuda(2) -> aplicando (1A) al revés: b = –a -> –ai = ±1/rzcuda(2) -> –a = ±1/i rzcuda(2) -> –a = ±– i/rzcuda(2) –> (2D) a = ±i/rzcuda(2)
Por lo tanto, aplicando (2A) y (2B) -> z = a + bi = ±1/rzcuda(2) ± i/rzcuda(2), y de forma redundante, aplicando (2C) y (2D) -> z = a + bi = ±i/rzcuda(2) ± 1/rzcuda(2) = ±1/rzcuda(2) ± i/rzcuda(2).
(Observe cómo las soluciones imaginarias de (2C) y (2D) coinciden con las soluciones reales de (2A) y (2B) al revers. El número de soluciones obtenido, 2, concuerda con el Teorema Fundamental del Álgebra: el número de soluciones de un polinomio es lo mismo que el grado del, o el exponente más alto en el, polinomio. En este caso, estamos tratando con una ecuación de segundo grado, por lo que hay exactamente 2 soluciones. Sin embargo, debido a a² – b² = 0 -> a² = b² y a = ±b, es posible resolver esto creando una ecuación de cuarto grado usando también 2ab = 1: b⁴ = 1/4 -> b = ±rz4a(1/4) = ±1/rzcuda(2), ±i/rzcuda(2). Sin embargo, esto crea un conjunto de soluciones engañoso en el que las soluciones positivas podrían mezclarse y combinarse con las negativas, ya que un polinomio de cuarto grado produciría 4 soluciones. Sin embargo, dado que la ecuación original es de segundo grado , solo hay 2 soluciones verdaderas donde los signos de las partes real e imaginaria coinciden, ya que los desajustes en esos signos darían –i en lugar de i).
Comprobando las 2 soluciones (2 pares de soluciones con cada par idéntico), obtenemos:
(1/rzcuda(2) + i/rzcuda(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i, y
(–1/rzcuda(2) – i/rzcuda(2))² = 1/2 + 2i/2 + i²/2 = 1/2 + i – 1/2 = i
PD Aquellos que estén interesados pueden ver cómo los diferentes signos entre las partes real e imaginaria producirían –i, en lugar de i, aquí hay una verificación de esas soluciones:
(1/rzcuda(2) – i/rzcuda(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – I – 1/2 = –i, y
(–1/rzcuda(2) + i/rzcuda(2))² = 1/2 – 2i/2 + i²/2 = 1/2 – i – 1/2 = –i
0 notes
Video
youtube
▶Suma de [POLINOMIOS] muy FÁCIL!! # 3
#polinomios algebraicos#suma de polinomios#algebra#algebra de baldor#clases de matematicas#trinomios#binomios#polinomios
2 notes
·
View notes
Text
Operaciones entre polinomios
Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales.
Podemos definir las operaciones de suma, resta, multiplicación y división entre polinomios como una generalización de las operaciones que hemos definido entre los números reales. Suma de polinomios Para sumar o restar polinomios, recurrimos a la propiedad asociativa de los números reales, pues agrupamos los sumandos que tengan la misma potencia de como factor, de forma que si consideramos dos…

View On WordPress
0 notes
Text
Un Amor muy "Matemático"
Un Cociente se enamoró de una incógnita.
Él, Cociente era producto de una familia de importantísimos polinomios. Ella, una simple incógnita de mezquina ecuación literal.
¡Oh! ¡Qué tremenda desigualdad!
Pero como todos saben, el amor no tiene límites y va del más infinito al menos infinito.
Embargado, el Cociente la contempló desde el vértice hasta la base, bajo todos los ángulos, agudos y obtusos. Era linda, una figura impar que se evidenciaba por: mirada romboidal, boca trapezoidal y senos esféricos en un cuerpo cilíndrico de líneas sinusoidales.
"¿Quién eres?", preguntó el Cociente con una mirada radical.
"Soy la raíz cuadrada de la suma de los cuadrados de los catetos, pero puedes llamarme Hipotenusa", contestó ella con expresión algebraica de quien ama.
Él hizo de su vida una paralela a la de ella, hasta que se encontraron en el infinito. Y se amaron hasta el cuadrado de la velocidad de la luz, dejando al sabor del momento y de la pasión, rectas y curvas en los jardines de la cuarta dimensión.
Él, la amaba y el recíproco era verdadero.
Se adoraban con las mismas razones y proporciones en un intervalo abierto de la vida.
Luego de tres cuadrantes, resolvieron casarse.
Trazaron planes para el futuro y todos le desearon felicidad integral. Los padrinos fueron el vector y la bisectriz.
Todo marchaba sobre ejes. El amor crecía en progresión geométrica. Cuando ella estaba en sus coordenadas positivas, concibió un par: al varón, en homenaje al padrino lo bautizaron Vector; la niña, una linda Abscisa. Ella fue objeto de dos operaciones.
Eran felices, hasta que un día todo se volvió una constante. Fue así que apareció otro. Sí, otro. El Máximo Común Divisor, un frecuentador de círculos viciosos. Lo mínimo que el Máximo ofreció fue de una magnitud absoluta.
Ella se sintió impropia, pero amaba al Máximo.
Al saber de esta regla de tres, el cociente la llamó fracción ordinaria.
Sintiéndose un denominador común, resolvió aplicar la solución trivial:
Un punto de discontinuidad.💑.
4 notes
·
View notes
Video
youtube
(vía https://www.youtube.com/watch?v=Uz2ChNh-hx8)
0 notes
Text
youtube
Reducir Polinomios De Distintas Clases Fracciones Distintos Signos En este vídeo aprenderás a reducir polinomios de diversas clases, con signos diferentes, coeficientes enteros y fraccionarios, agrupar por términos semejantes.
#reducción de términos semejantes#matematicas#polinomios#algebra#matemáticas#reduccion de terminos semejantes#suma#semejantes#agrupar terminos semejantes#agrupar terminos semejantes y simplifica#simplificar#propiedad asociativa#propiedad conmutativa#resta#potencia#exponente litereal#polinomios fraccionarios#polinomios enterios#coeficiente entero#termino independiente#termino no semejante#polinomio de segundo grado#polinomios de segundo grado ejercicios resueltos#Youtube
0 notes
Text
Un cociente se enamoró de una incógnita. Él cociente era producto de una familia de importantísimos polinomios. Ella una simple incógnita de mezquina ecuación literal ¡oh! ¡Qué tremenda desigualdad!
Pero como todos saben, el amor no tiene límites y va del más infinito al menos infinito.
Embargado, el cociente la contempló desde el vértice hasta la base, bajo todos los ángulos, agudos y obtusos. Era linda, una figura impar que se evidenciaba por: mirada romboidal, boca trapezoidal y senos esféricos en un cuerpo cilíndrico de líneas sinusoidales.
"¿Quién eres?", preguntó el cociente con una mirada radical.
"Soy la raíz cuadrada de la suma de los cuadrados de los catetos, pero puedes llamarme hipotenusa", contestó ella con expresión algebraica de quien ama.
Él hizo de su vida una paralela a la de ella, hasta que se encontraron en el infinito. Y se amaron hasta el cuadrado de la velocidad de la luz, dejando al sabor del momento y de la pasión, rectas y curvas en los jardines de la cuarta dimensión.
Él la amaba y el recíproco era verdadero. Se adoraban con las mismas razones y proporciones en un intervalo abierto de la vida.
Luego de tres cuadrantes, resolvieron casarse.
Trazaron planes para el futuro y todos le desearon felicidad integral. Los padrinos fueron el vector y la bisectriz.
Todo marchaba sobre ejes. El amor crecía en progresión geométrica. Cuando ella estaba en sus coordenadas positivas, concibió un par: al varón, en homenaje al padrino lo bautizaron vector; la niña, una linda abscisa. Ella fue objeto de dos operaciones.
Eran felices, hasta que un día todo se volvió una constante. Fue así que apareció otro. Sí, otro. El máximo común divisor, un frecuentador de círculos viciosos. Lo mínimo que el máximo ofreció fue de una magnitud absoluta.
Ella se sintió impropia, pero amaba al máximo. Al saber de esta regla de tres, el cociente la llamó fracción ordinaria.
Sintiéndose un denominador común, resolvió aplicar la solución trivial: un punto de discontinuidad.
Si entendiste algo eres un intelectual. Si no lo entendiste. Perdiste tu tiempo en el colegio.
¡Genial!
¿Quién será el autor?
#likejvg #maracaibo #zulia #venezuela #peru #lima #santaclaraate #mcbo #instagood #photooftheday #fashion #beautiful #happy #cute #emprendedor #unlogroalavez #love #emprendimiento #varela #jvg #motivacion #actitud #mentesmillonarias #aptitud #exito #influencer #empresarios #bitcoin #trading #trader @jvarelag
0 notes
Photo

Un Cociente se enamoró de una Incógnita. El Cociente era producto de una familia de importantísimos polinomios. Ella, una simple incógnita de mezquina ecuación lineal. ¡Oh! ¡Qué tremenda desigualdad! Pero como todos saben, el amor no tiene límites y va del cero al infinito. Enamorado y embelesado, el Cociente le había contemplado desde el vértice hasta la base; desde su perspectiva, admiró todos los ángulos: agudos y obtusos, pero el recto lo vislumbró. Ella contorneaba su linda figura; una figura impar y absoluta, de mirada romboidal, boca trapezoidal y senos esféricos en un cuerpo cilíndrico de líneas sinusoidales, que guardaban celosamente lo mas preciado de ella . . . su circulito. "¿Quién eres?", preguntó el Cociente con una mirada radical. "Soy la raíz cuadrada de la suma de los cuadrados de los catetos, pero puedes llamarme Hipotenusa", contestó ella con expresión algebraica de quien ama integralmente. Él fue construyendo una vida paralela a la de ella, hasta que el infinito provocó su encuentro. Y se amaron hasta el cuadrado de la velocidad de la luz, dejando al sabor del momento y de la pasión, rectas y curvas en los jardines de la cuarta dimensión. Él, la amaba con frenesí y anhelaba que este sentimiento no tuviera diferencial, que fuese recíproco y verdadero. Se adoraban con las mismas razones y proporciones en un intervalo abierto de la vida. Luego de tres cuadrantes, resolvieron casarse. Trazaron planes para el futuro y todos le desearon felicidad integral. Los padrinos fueron el vector y la bisectriz. Todo marchaba sobre ejes. El amor crecía en progresión geométrica. Cuando ella estaba en sus coordenadas positivas, fue objeto de dos operaciones, concibiendo así un par de derivadas: Al varón, en homenaje al padrino lo bautizaron con el nombre de Vector y a la niña Abscisa por hermosa y concéntrica. Todo era felicidad en ese mundo de conjuntos y relaciones, hasta que el tiempo convirtió a la relación en una monótona constante. La necesidad de una variable en la relación fué evidente y fué ahí donde apareció el Máximo Común Divisor, un frecuentador de círculos viciosos. (No es mío) y aún no acaba. https://www.instagram.com/p/CVB2-ECr7RB/?utm_medium=tumblr
0 notes
Text
Funciones y polinomios / 1. Dominio y gráfica de una función
Funciones Una expresión algebraica cuyo valor depende solamente del valor que tome una variable independiente se llama función de , . Si la función es del tipo se llama polinómica. Por su parte, la expresión , formada por una suma de potencias de multiplicadas por determinados coeficientes , , , es un polinomio de grado Dada la función polinómica , su valor depende del que le demos a la…

View On WordPress
0 notes
Video
youtube
Identificación, Suma y Resta de Polinomios
0 notes
Text
Suma de fracciones algebraicas
1.Calcular MCM de los denominadores que da el ejercicio.
2. Se coloca el MCM como denominador.
Se compara en denominador de la primera fracción que dan en el ejercicio y veo que le hace falta para ser como el MCM, ese dato que es el faltante se debe poner en paréntesis a la par del primer numerador y lo mismo con las demás fracciones.
3. Multiplicar el numerador que ya me daban con el faltante que se colocó en paréntesis. Hacer esto con todos los numeradores y su faltante.
4. Se hace suma y/o de polinomios. (No olvides, términos semejantes)
5. Factorizar si es posible.
(No olvides que después de factorizar una vez puedes volver a hacerlo si se diera la oportunidad, lo importante es llevarlo a lo más mínimo)

0 notes